“ECUACIONES DE SEGUNDO GRADO”
A. Encuadre
E. Descripción del Contenido de la Unidad IV “ Ecuaciones de Segundo Grado”
4.1. Ecuaciones de segundo grado
• Método algebraico: Despeje de ecuaciones incompletas, Factorización y formula general
El estudiante resolverá situaciones y problemas en los que se apliquen ecuaciones de segundo grado con una incógnita, empleando el método algebraico y su interpretación grafica analizando las soluciones reales e imaginarias, conservando el respeto y la calidad de sus trabajos.
• El estudiante resolverá un examen diagnostico que indique el nivel de aprendizaje que tiene en ese momento y los temas que tendrá que reforzar para iniciar este curso.
• El estudiante leerá el material, analizará y resolverá los ejemplos con los que cuenta.
• El estudiante después de estudiar los principios de la aritmética así como la importancia de la simbología en el álgebra y la clasificación de los números reales, resolverá las actividades de consolidación, que le permitan reafirmar el aprendizaje.
• Al final de la unidad el estudiante mandará al asesor la serie los ejercicios y actividades complementarias contenidas en este material para su evaluación.
• Se le propone al estudiante ir verificando la solución de los ejercicios propuestos en la parte de “solución a los ejercicios propuestos”
• El estudiante resolverá los ejercicios propuestos en el material y los enviará al asesor para su evaluación
• El estudiante analizará y resolverá las actividades de consolidación haciendo comentarios y/o observaciones si lo considera oportuno.
• Los trabajos enviados al asesor tendrá un valor máximo del 50% del total de la calificación.
• El otro 50% restante será la valoración del examen, por medio de la prueba objetiva.
EXAMEN DIAGNOSTICO DE LA UNIDAD IV
• Para cada una de las siguientes ecuaciones determina el valor de x que satisfaga la ecuación:
• 
• 
• 
• Para cada una de las ecuaciones de este bloque, determina si sus soluciones son las que se presentan:
• 
• 
• 
• Encuentra los binomios conjugados para cada uno de las diferencias de cuadrados siguientes:
• 
• 
• 
• Determina el trinomio cuadrado perfecto para cada uno de los siguientes casos;
• 
• 
• 
• Factoriza cada uno de los trinomios siguientes:
• 
• 
• 
SOLUCION DEL EXAMEN DIAGNOSTICO DE LA UNIDAD IV
1)
• 
• 
• 
2)
• 
b) 
c) 
3)
a) 
b) 
c) 
4)
a) 
b) 
c) 
5)
a) 
b) 
c) 
4.1 Ecuaciones de segundo grado
Recordando algunos conceptos:
- Ecuación: “Es una igualdad que contiene una o varias incógnitas elevadas a la n potencia”
- Resolución de ecuaciones: “Es encontrar el valor o valores de las incógnitas que contiene la igualdad para que al sustituirlas en la misma ésta se cumpla, dicho de otra manera, encontrar los valores de las incógnita que satisfacen a la igualdad”
- La ecuación es un planteamiento matemático que nos permite resolver problemas, también conocido como modelo matemático.
En esta unidad analizaremos las ecuaciones de segundo grado con una incógnita, de acuerdo con las definiciones anteriores, analizaremos una igualdad que contenga una incógnita elevada al cuadrado (segunda potencia). Una ecuación de éste tipo se expresa por:
Encontrar el valor de la incógnita (x) implica el uso de métodos que me permitan saber ese valor que hace que la igualdad se cumpla.
En el caso de las ecuaciones de segundo grado, a diferencia de las de primer grado, la mayoría de éstas tienen dos valores que satisfacen a la igualdad, llamados raíces de la ecuación.
Las ecuaciones de segundo grado con una incógnita tienen las siguientes formas:
Forma completa; 
Forma incompleta: ax² + bx = 0, a ? 0
Forma incompleta: ax² + c = 0, a ? 0
Donde a, b y c son coeficientes conocidos y x la incógnita, lo desconocido.
La forma completa tiene tres términos; “ax²” el cuadrático, “bx” el lineal y “c” el independiente. Mientras que en las incompletas se carece de uno de ellos, excepto el cuadrático.
Casos de despeje, Factorización y formula general
INTRODUCCIÓN . La forma general de una ecuación de segundo grado con una incógnita, polinomio de grado dos, es: 
Estamos hablando de la forma estándar de un polinomio de segundo grado, un polinomio completo. Algunos ejemplos de estos son:
Observa que, en la forma estándar de un polinomio de grado dos, tenemos tres términos: el elemento de potencia dos, el elemento de potencia uno y el elemento libre. Se trata pues de un trinomio, es decir un polinomio de tres términos. En todos los ejemplos anteriores presentamos polinomios cuadráticos completos, en su forma estándar.
Hablar de la solución de una ecuación de segundo grado es encontrar los valores de la variable x, que satisfagan la ecuación; esto es, encontrar los valores de x que al ser sustituidos en una ecuación determinada, el resultado de esta evaluación nos de igual a cero.
Ejemplo. La ecuación 
, tiene dos soluciones 
y 
; al sustituir cada uno de estos valores en la ecuación tenemos que:
Para 
y para 
Veremos que una ecuación de segundo grado puede tener dos soluciones distintas, como en el ejemplo anterior, dos soluciones iguales o bien no tener soluciones.
El caso segundo, de dos soluciones iguales, puede verse en la ecuación 
, en donde su única solución (equivalente a dos soluciones iguales) es 
. Por otro lado un ejemplo de ecuación de segundo grado sin solución es 
. Se tiene que hacer la advertencia que no tiene soluciones en el campo de los números reales y sí en cambio en el campo de los números complejos. Esto tomará significado cuando se hable de este aspecto.
SOLUCIÓN ANALÍTICA DE UNA ECUACION DE SEGUNDO GRADO.
Recordemos la forma general de esta ecuación de segundo grado: 
y vallamos en búsqueda de métodos analíticos para su solución; para esto observemos los tres distintos casos que pueden darse en esta ecuación, de acuerdo a la cantidad de términos que contenga:
CASO 1 |
ax 2 |
0 |
c |
=0 |
CASO 2 |
ax 2 |
bx |
0 |
=0 |
CASO 3 |
ax 2 |
bx |
c |
=0 |
Por supuesto que el tercer caso pudiera parecer el mas complejo, porque este tiene sus tres coeficientes (a, b, c) distintos de cero. Comencemos por el caso más simple, el CASO 1:
Para resolver la ecuación: 
, basta con hacer los siguientes despejes:
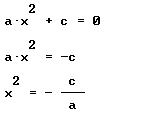
y tenemos que las dos soluciones de esta ecuación son:
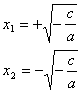
Observemos la condición de que el radical deberá ser positivo para que tenga solución en los números reales (en realidad también puede ser cero, es decir 
) de lo contrario tendría solución únicamente en el campo de los números complejos.
Ejemplo . Encontremos las soluciones de la siguiente ecuación cuadrática 
.
Hagamos el trabajo algebraico siguiente
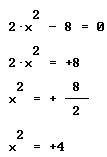
y finalmente la soluciones de esta ecuación son las siguientes:
Ejemplo . Encontremos las soluciones de la ecuación 
. De manera similar al ejemplo anterior, hagamos el trabajo siguiente:
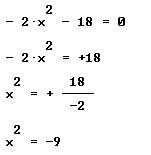
Esta ultima expresión se puede poner de la siguiente manera: 
. Esta ultima expresión nos permite ver que nuestra ecuación no tiene soluciones reales, esto porque el radical contiene un numero negativo. Recuerda que la raíz cuadrada de un número negativo no existe; esto es distinto en los números complejos.
EJERCICIOS CASO1 . Encontrar las soluciones de cada una de las ecuaciones siguientes.
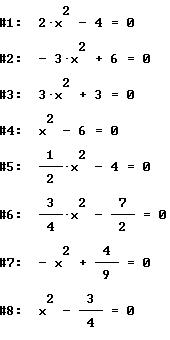
Soluciones de los primeros cuatro ejercicios, caso1:
1: 
2: 
3: 
4: 
MÉTODO ALTERNATIVO, CASO1. Una manera más de darle solución a este tipo de polinomios es la siguiente, la cual me permitiré mostrar con el ejemplo que ha sido desarrollado anteriormente, para la ecuación 
:
• Primero, dividamos la ecuación entre el coeficiente que tenga el termino cuadrático, en este caso el 2 y obtenemos la expresión: 
.
• Segundo, transformemos la anterior expresión a una diferencia de cuadrados, obteniendo la expresión: 
• Tercero, recordando el concepto de productos notable, la expresión anterior puede factorizarse como un producto de binomios conjugados: 
.
• Cuarto, las soluciones, son aquellos valores de x que hacen a cada uno de los factores (los paréntesis) igual a cero; por lo que, para el ejemplo, son 
y 
.
EJERCICIOS CASO 1. Como ejercicios, podrían realizarse los del bloque anterior de ejercicios, bajo esta alternativa, es decir aplicando el método alternativo. Compara los resultados y la facilidad de obtención en ambos casos.
METODO DE SOLUCION, CASO 2.
Para darle solución a estas ecuaciones, de la forma 
, en donde el término independiente es cero (c=0), aplicaremos el siguiente trabajo algebraico:
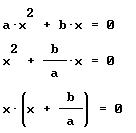
Lo anterior se obtiene, dividiendo por a toda la ecuación, y factorizando una x; así, la solución lógica, llamada solución trivial, es 
. El contenido del paréntesis nos permite ver que se convierte en cero cuando 
, lo cual nos daría la segunda solución. Resumiendo, para este caso, las soluciones son de la forma:
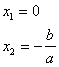
En donde la primera solución, la trivial, siempre se presenta como solución.
Ejemplo . Encontrar las soluciones de la ecuación 
. Puedes identificarla con el caso 2, dado que carece del término independiente, hagamos lo indicado:
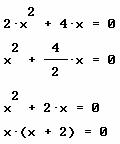
Finalmente las soluciones de esta ecuación, son las que hacen cero a cada uno de los factores:
Ejemplo . Determinar las soluciones de la siguiente ecuación cuadrática 
.
En este caso, el trabajo algebraico, se simplifica dado que el elemento cuadrático posee un coeficiente de uno, por tanto la solución se reduce a la Factorización:
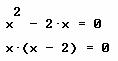
Por lo que las soluciones son:
Ejemplo . Cuáles son las soluciones para el caso de la ecuación 
.
Aplicando el procedimiento para el caso 2:
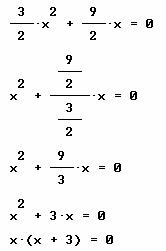
Por lo que las soluciones son:
NOTA. Observa como en estos ejemplos, del caso 2, siempre se presenta la solución trivial, la solución 
.
EJERCICIOS CASO 2. Encuentra las soluciones para cada una de las ecuaciones siguientes. Recuerda que si el término independiente es cero siempre se presentará la solución trivial para tus ecuaciones.
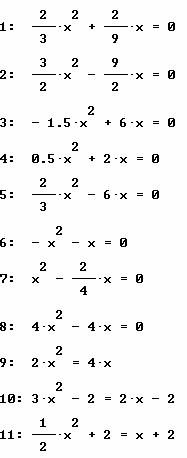
Soluciones de las primeras 5 ecuaciones, caso 2.
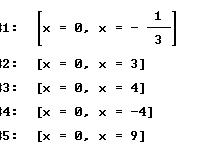
METODO DE SOLUCION, CASO 3.
Para este caso, en que se tenga un polinomio con todos sus términos, 
, es decir un trinomio cuadrático, el método propuesto sugiere formar un trinomio cuadrado perfecto, con los primeros dos términos, esto como parte central del método y como punto de partida del mismo. Nos permitimos presentar el método aplicándolo a la ecuación 
:
• Primero dividamos la ecuación entre el coeficiente del término cuadrático y obtendremos un polinomio equivalente:
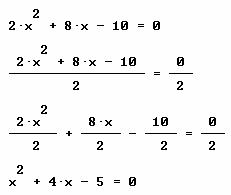
• Agrupar los primeros dos términos , 
, y formar con ellos un trinomio cuadrado perfecto; recuerda que esto se logra sumando un número que resulta de dividir el 4 entre dos y el resultado elevarlo al cuadrado, es decir un 4 para este caso:
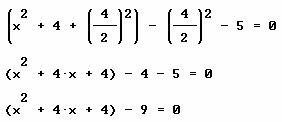
Por supuesto que lo que se suma, para formar el trinomio cuadrado perfecto, se debe restar en la misma ecuación para mantener el equilibrio, para mantener la igualdad.
• El trinomio cuadrado perfecto puede sustituirse como un binomio al cuadrado, de ahí la intención de crear este trinomio:
• El siguiente trabajo algebraico ya lo conoces, es muy parecido al caso 1, y habrá de seguirse para encontrar las soluciones:
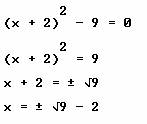
Debemos poner atención en la raíz, 
, que se trata de la raíz de un número positivo y esta es la condición para que existan soluciones de la ecuación, las cuales se desprenden de la expresión : 
• Finalmente, las soluciones son:
NOTA. Estamos seguros que esta propuesta, para el caso3, este método de solución, puede ser adecuada por ti; el trabajo de los productos notables puede ser utilizado para darle variantes al trabajo algebraico propuesto para ti en este método de solución.
Ejemplo. Determina las soluciones de la ecuación cuadrática siguiente: 
.
• Agrupar los primeros dos términos , 
, y formar con ellos un trinomio cuadrado perfecto:
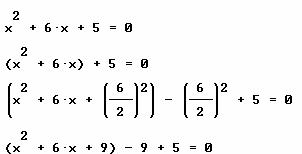
Simplificando la última expresión, tenemos:
• Sustituimos el trinomio cuadrado perfecto por un binomio al cuadrado:
• Hacemos los despejes necesarios para obtener la propuesta :
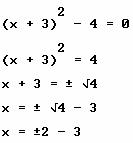
• Finalmente, las soluciones son:
NOTA. Insistimos que este trabajo algebraico es solo una propuesta que puede ser seguida y considerar las variantes que tú puedas dar.
EJERCICIOS CASO 3. Encuentra las soluciones para cada una de las ecuaciones siguientes.
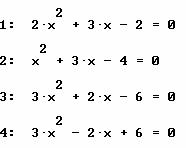
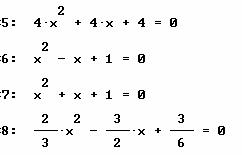
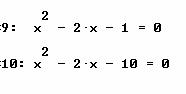
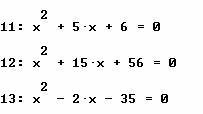
Solución de las primeras 6 ecuaciones, caso 3.
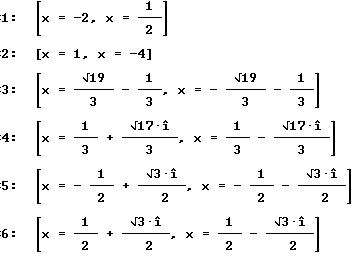
FORMULA GENERAL DE SEGUNDO GRADO . El uso de esta fórmula, para encontrar las soluciones de una ecuación de segundo grado, puede utilizarse como una forma alternativa de solución para los tres casos que hemos trabajado. Esta fórmula se genera del trabajo con los coeficientes de la ecuación, de manera similar a como se propone para el tercer caso. La fórmula que presentamos como alternativa de solución para la ecuación de la forma 
es la siguiente:
El uso de esta ecuación, que no tiene mas que la sustitución de los coeficientes de la ecuación, la mostramos con el siguiente ejemplo:
Ejemplo. Encontrar las soluciones de la ecuación cuadrática 
utilizando la fórmula general de segundo grado. Recuerda que esta ecuación ya ha sido resuelta en el método del caso3.
• Reconozcamos, primeramente, los coeficientes de nuestra ecuación, comparándolos con los de la forma general de segundo grado; esto nos arroja lo siguiente:
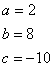
• Sustituir cada uno de los valores en la fórmula y hacer las operaciones aritméticas que se requieran.
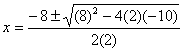
• Finalmente las dos soluciones que tiene nuestra ecuación, se obtienen con esta expresión y son las siguientes:
Ejemplo . Encontremos las soluciones de la ecuación siguiente 
.
• Identifiquemos los coeficientes de la ecuación:
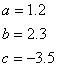
• Hacemos todas las sustituciones en la fórmula general:
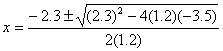
• Las soluciones son:
NOTA. La propuesta para el uso de esta fórmula de segundo grado, en dónde realmente se agradece su existencia, es para este último tipo de ecuaciones, en donde los coeficientes son cantidades decimales.
En la fórmula para resolver ecuaciones cuadráticas, al subradical (b 2 – 4ac) se le llama Discriminante ya que permite conocer la naturaleza de las raíces de una ecuación con base en los criterios siguientes:
Si (b 2 – 4ac) > 0, las raíces son reales y diferentes.
Si (b 2 – 4ac) = 0, las raíces son reales e iguales.
Si (b 2 – 4ac) < 0, las raíces son complejas.
Ejemplos : Ecuación Discriminante (b 2 – 4ac).
x 2 – 7x + 10 = 0 (7) 2 – 4(1)(10) = 49 – 40 = 9 raíces reales y diferentes
x 2 + 6x + 9 = 0 (6) 2 – 4(1)( 9) = 36 – 36 = 0 raíces reales e iguales
x 2 – 4x + 8 = 0 (– 4) 2 – 4(1)(8) = 16 – 32 = –16 raíces complejas.
Ejercicios : Resolver cada ecuación por la fórmula general:
• x 2 + 8x + 15 = 0
• x 2 + 10x + 16 = 0
• x 2 + 6x + 5 = 0
• x 2 – 5x + 6 = 0
• x 2 – x – 2 = 0
• x 2 – 14x + 49 = 0
• x 2 – 2x + 2 = 0
• x 2 + 8x + 16 = 0
• x 2 – 2x + 1 = 0
• 3x 2 – 5x + 4 = 0
EJERCICIOS, FÓRMULA GENERAL DE SEGUNDO GRADO.
Se propone aplicar la fórmula en algunos de los casos sugeridos en los distintos bloques de ejercicios propuestos; procura resolver ecuaciones de los tres bloques de ejercicios y no olvides comparar esos resultados con los que te arroje el uso de la fórmula general; sumado a ello te proponemos realices los siguientes ejercicios utilizando la formula general, para lo que te sugerimos tengas a la mano una calculadora para realizar las operaciones a que te enfrentaras:
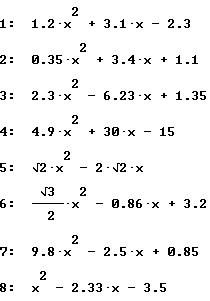
Solución de las primeras 4 ecuaciones, utilizando la formula general:
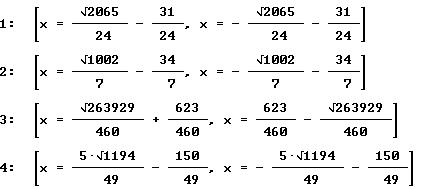
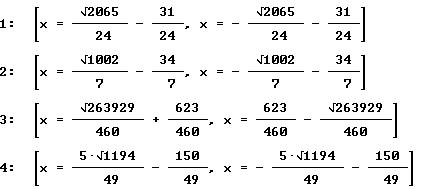
Las ecuaciones cuadráticas también se pueden resolver realizando la gráfica de la ecuación.
Al realizar la grafica se observa el lugar por donde cruza la grafica al eje de las abscisas (X)
La actividad siguiente se recomienda suponer valores para la variable X y obtener los de Y, esto en una tabla, posteriormente se grafica en un sistema de coordenadas rectangulares y se observa el comportamiento de la curva, que en este caso es una parábola que puede cruzar al eje de las X.
El lugar por donde cruza en el eje de las abscisas es el valor que satisface a la ecuación
ACTIVIDAD: graficar las siguientes ecuaciones
• y = x² + 11x +24 Sol. – 3 y - 8
• y = x² - 16x + 63 Sol 7 y 9
• y = 3x²- 48 Sol ± 4
• y = 5x² - 9 – 46 Sol ± v11
• y = x² - 5x Sol 0, 5
• y = 4x² + 32x Sol 0, - 8
- Carpintero, V., Eduardo y Sánchez H, Rubén B. “Álgebra”. México, Publicaciones cultural 2002
- Carreño campos Ximena “álgebra”. México publicaciones culturales 2003
- Cuellar José A. “Matemáticas I para bachillerato”. México, McGraw Hill 2003
- Kaseberg Alice “álgebra elemental”. México, ediciones Thomson internacional, 2001
- Pantoja Ayala Salvador Gabriel, “Apuntes de matemáticas I” SEA Zamora
- Smith, Stanley y col “álgebra”. EUA., Addison-Wesley IberoAmérica, 2001
- Baldor, A. “Álgebra” publicaciones cultural.