A.- ENCUADRE.
B.- OBJETIVO DE LA UNIDAD.
C.-CONTENIDO TEMATICO
D.-BIBLIOGRAFIA.
La primera Unidad incluye contenidos sobre la metodología para solucionar problemas, a través de la elaboración de diagramas y el desarrollo de algoritmos.
La asignatura de Informática II se imparte en segundo semestre y apoya a las diversas asignaturas del plan de estudios, al proporcionar herramientas para el desarrollo de materiales educativos.
B.- OBJETIVOS DE LA UNIDAD I
.
GENERALEl estudiante:
Desarrollará algoritmos, mediante el empleo de diagramas de flujo en la solución de problemas elementales del ámbito escolar y de la vida cotidiana, propiciando soluciones creativas.
ESPECÍFICOS:
El estudiante:
1.1. Explicará la importancia del empleo de algoritmos en la solución de problemas elementales del ámbito escolar y de la vida cotidiana, a través de la revisión de sus características y aplicabilidad.
1.2. Aplicará una metodología en la solución de problemas, mediante el razonamiento deductivo y la conceptualización de cada una de sus etapas.
1.3. Desarrollará diagramas de entrada proceso salida y de flujo en la solución de problemas elementales y de la vida cotidiana, mediante la revisión de ejemplos de sus usos y aplicación.
1.1. Terminología empleada en algoritmos.
1.1.1. Definición de problema.
1.1.2. Definición de algoritmo.
1.1.3. Características de los algoritmos.
1.1.4. ACTIVIDADES DE REFORZAMIENTO1.2. Metodología de solución de problemas.
1.2.1. Identificación del problema.
1.2.2. Planteamiento de alternativas de solución.
1.2.3. Elección de una alternativa.
1.2.4. Desarrollo de la solución.
1.2.5. Evaluación de la solución.
1.2.6. ACTIVIDADES DE REFORZAMIENTO1.3.1. Diagramas de entrada-proceso-salida.
1.3.2. Diagramas de flujo.
1.3.3. Ejemplos de usos y aplicación.
1.3.4. ACTIVIDADES DE REFORZAMIENTO1.1. Terminología empleada en algoritmos.
La principal razón para que las personas aprendan lenguajes de programación es utilizar la computadora como una herramienta para la solución de problemas.
Dos fases pueden ser identificadas en este proceso.
1- Fase de resolución del problema.
2- Fase de implementación en una microcomputadora.El resultado de la primera fase es el diseño de un algoritmo para resolver el problema. Un algoritmo se puede considerar como el conjunto de instrucciones que conducen a la solución de un problema determinado. Dichas instrucciones deben tener una secuencia lógica para poder llegar a la solución real. El algoritmo se puede expresar de diversas maneras. Mediante símbolos, utilizando un lenguaje determinado para hablar la solución, describir sintéticamente dicho lenguaje de programación. La última forma de describir el algoritmo es a lo que se denomina PROGRAMA.
1.1.1. Definición de problema.
- Clasificación de problemas
Los problemas matemáticos se pueden dividir en primera instancia en dos grupos:
* Problemas indecidibles: aquellos que no se pueden resolver mediante un algoritmo.
* Problemas decidibles: aquellos que cuentan al menos con un algoritmo para su cómputo.Sin embargo, que un problema sea decidible no implica que se pueda encontrar su solución, pues muchos problemas que disponen de algoritmos para su resolución son inabordables para un computador por el elevado número de operaciones que hay que realizar para resolverlos. Esto permite separar los problemas decidibles en dos:
* intratables: aquellos para los que no es factible obtener su solución.
* tratables: aquellos para los que existe al menos un algoritmo capaz de resolverlo en un tiempo razonable.
Los problemas pueden clasificarse también atendiendo a su complejidad. Aquellos problemas para los que se conoce un algoritmo polinómico que los resuelve se denominan clase P. Los algoritmos que los resuelven son deterministas. Para otros problemas, sus mejores algoritmos conocidos son no deterministas. Esta clase de problemas se denomina clase NP. Por tanto, los problemas de la clase P son un subconjunto de los de la clase NP, pues sólo cuentan con una alternativa en cada paso.Un cierto problema tiene solución algorítmica de complejidad lineal cuando el costo de la solución crece en forma proporcional con la cantidad de datos. Por ejemplo, en el método de búsqueda del máximo valor de un conjunto de números, la solución tarda un cierto tiempo promedio, que depende linealmente de la cantidad de elementos en la lista, por que le programa ocupa, por ejemplo, diez veces más tiempo en encontrar el número mayor en la lista de longitud 100 que en una de longitud 10.
Un problema tiene solución algorítmica de complejidad polinominal (que es peor en términos generales que la lineal) cuando la ecuación que describe el costo de la solución es un polinomio (y no una simple variable o una constante), que suele crecer bastante más rápido que una ecuación lineal sencilla.
Un algoritmo es de complejidad exponencial cuando la ecuación que describe su comportamiento tiene exponentes variables, con lo que el costo de la ejecución del programa se puede disparar y hacerse inmanejable para ciertos tamaños en la longitud de los datos que maneja.
Por último, los algoritmos inherentemente complejos exhiben tal velocidad de crecimiento en su costo de ejecución que resultan del todo impensables, aun para las más poderosas supercomputadoras.
1.1.2. Definición de algoritmo.
Un algoritmo es el método que emplea un programa para llegar a su fin y, en términos práctica, constituye el “cómo” funciona una descripción.
En general, de un algoritmo se pueden decir muchas cosas, entre las cuales destaca si es correcto o no (o sea, si cumple o no con su objetivo de describir algo); qué tan eficiente es (cuánto tarda en llegar a su fin, o bien cuántas celdas de memoria requiere); qué tan elegante es(es decir, si sigue un camino inteligente o bien planteado para efectuar su trabajo, sin dar rodeos innecesarios o sin emplear recursos superfluos); qué tan claro es, y otras.
La especificación formal de un algoritmo en términos primitivos o elementales es una tarea eminentemente teórica y de gran interés matemático, porque resulta que existen varias categorías de ellos, de acuerdo con su complejidad: algoritmos lineales, polinominales, exponenciales, e “inherentemente complejos”.
Una definición informal (no se considera aquí una definición formal, aunque existe): conjunto finito de reglas que dan una secuencia de operaciones para resolver todos los problemas de un tipo dado. De forma más sencilla, podemos decir que un algoritmo es un conjunto de pasos que nos permite obtener un dato. Además debe cumplir estas condiciones:• Finitud: el algoritmo debe acabar tras un número finito de pasos. Es más, es casi fundamental que sea en un número razonable de pasos.
• Definibilidad: el algoritmo debe definirse de forma precisa para cada paso, es decir, hay que evitar toda ambigüedad al definir cada paso. Puesto que el lenguaje humano es impreciso, los algoritmos se expresan mediante un lenguaje formal, ya sea matemático o de programación para un computador.
• Entrada: el algoritmo tendrá cero o más entradas, es decir, cantidades dadas antes de empezar el algoritmo. Estas cantidades pertenecen además a conjuntos especificados de objetos. Por ejemplo, pueden ser cadenas de caracteres, enteros, naturales, fraccionarios, etc. Se trata siempre de cantidades representativas del mundo real expresadas de tal forma que sean aptas para su interpretación por el computador.
• Salida: el algoritmo tiene una o más salidas, en relación con las entradas.
• Efectividad: se entiende por esto que una persona sea capaz de realizar el algoritmo de modo exacto y sin ayuda de una máquina en un lapso de tiempo finito.A menudo los algoritmos requieren una organización bastante compleja de los datos, y es por tanto necesario un estudio previo de las estructuras de datos fundamentales. Dichas estructuras pueden implementarse de diferentes maneras, y es más, existen algoritmos para implementar dichas estructuras. El uso de estructuras de datos adecuadas pueden hacer trivial el diseño de un algoritmo, o un algoritmo muy complejo puede usar estructuras de datos muy simples.
Uno de los algoritmos más antiguos conocidos es el algoritmo de Euclides. El término algoritmo proviene del matemático Muhammad ibn Musa al-Khwarizmi, que vivió aproximadamente entre los años 780 y 850 d.C. en la actual nación Iraní. El describió la realización de operaciones elementales en el sistema de numeración decimal. De al-Khwarizmi se obtuvo la derivación algoritmo.
1.1.3. Características de los algoritmos.- Clasificación de algoritmos
* Algoritmo determinista: en cada paso del algoritmo se determina de forma única el siguiente paso.
* Algoritmo no determinista: deben decidir en cada paso de la ejecución entre varias alternativas y agotarlas todas antes de encontrar la solución.Todo algoritmo tiene una serie de características, entre otras que requiere una serie de recursos, algo que es fundamental considerar a la hora de implementarlos en una máquina. Estos recursos son principalmente:
• El tiempo: período transcurrido entre el inicio y la finalización del algoritmo.
• La memoria: la cantidad (la medida varía según la máquina) que necesita el algoritmo para su ejecución.Obviamente, la capacidad y el diseño de la máquina pueden afectar al diseño del algoritmo.
En general, la mayoría de los problemas tienen un parámetro de entrada que es el número de datos que hay que tratar, esto es, N. La cantidad de recursos del algoritmo es tratada como una función de N. De esta manera puede establecerse un tiempo de ejecución del algoritmo que suele ser proporcional a una de las siguientes funciones:
• 1 : Tiempo de ejecución constante. Significa que la mayoría de las instrucciones se ejecutan una vez o muy pocas.
• logN : Tiempo de ejecución logarítmico. Se puede considerar como una gran constante. La base del logaritmo (en informática la más común es la base 2) cambia la constante, pero no demasiado. El programa es más lento cuanto más crezca N, pero es inapreciable, pues logN no se duplica hasta que N llegue a N2.
• N : Tiempo de ejecución lineal. Un caso en el que N valga 40, tardará el doble que otro en que N valga 20. Un ejemplo sería un algoritmo que lee N números enteros y devuelve la media aritmética.
• N-logN : El tiempo de ejecución es N-logN. Es común encontrarlo en algoritmos como Quick Sort y otros del estilo divide y vencerás. Si N se duplica, el tiempo de ejecución es ligeramente mayor del doble.
• N2 : Tiempo de ejecución cuadrático. Suele ser habitual cuando se tratan pares de elementos de datos, como por ejemplo un bucle anidado doble. Si N se duplica, el tiempo de ejecución aumenta cuatro veces. El peor caso de entrada del algoritmo Quick Sort se ejecuta en este tiempo.
• N3 : Tiempo de ejecución cúbico. Como ejemplo se puede dar el de un bucle anidado triple. Si N se duplica, el tiempo de ejecución se multiplica por ocho.
• 2N : Tiempo de ejecución exponencial. No suelen ser muy útiles en la práctica por el elevadísimo tiempo de ejecución. El problema de la mochila resuelto por un algoritmo de fuerza bruta -simple vuelta atrás- es un ejemplo. Si N se duplica, el tiempo de ejecución se eleva al cuadrado.
* Algoritmos polinomiales: aquellos que son proporcionales a Nk. Son en general factibles.
* Algoritmos exponenciales: aquellos que son proporcionales a kN. En general son infactibles salvo un tamaño de entrada muy reducido.1.1.4. ACTIVIDADES DE REFORZAMIENTO
1.2. Metodología de solución de problemas.
Debido a su propia naturaleza, la programación implica una gran cantidad de conceptos interrelacionados. Esto supone una dificultad para la gente que está aprendiendo a programar porque no puede comprender un determinado concepto sin entender previamente otros. Y tampoco podrá entender aquellos si no comprende el primero. La mejor solución implica el aprendizaje mediante la práctica y de forma incremental. Aprender de forma incremental significa que primero deberá aprender un poco sobre determinados temas y, a continuación, deberá seguir aprendiendo más sobre dichos temas y así sucesivamente, siempre aumentando el nivel de detalle. De alguna manera, la programación nunca termina; los programadores y técnicos con décadas de experiencia siguen descubriendo matices y refinando sus técnicas.
1.2.1. Identificación del problema.
Casi inconscientemente, los humanos efectuamos cotidianamente una serie de pasos, procedimientos o acciones que nos permiten alcanzar un resultado o resolver un problema.
Esta serie de pasos, procedimientos o acciones, comenzamos a aplicarlas muy temprano en la mañana cuando, por ejemplo, decidimos tomar un baño. Posteriormente cuando pensamos en desayunar también seguimos una serie de pasos que nos permiten alcanzar un resultado específico: tomar el desayuno. La historia se repite innumerables veces durante el día. Continuamente seguimos una serie de pasos o conjunto de acciones que nos permiten alcanzar un resultado. Estamos en realidad aplicando un algoritmo para resolver un problema.
Formalmente definimos un algoritmo como un conjunto de pasos, procedimientos o acciones que nos permiten alcanzar un resultado o resolver un problema.
Muchas veces aplicamos el algoritmo de manera inadvertida, inconscientemente o automáticamente. Esto generalmente se produce cuando el problema que tenemos enfrente lo hemos resuelto con anterioridad un gran número de veces.
Supongamos que simplemente tenemos que abrir una puerta. Lo hemos hecho tantas veces que difícilmente nos ponemos a enumerar los pasos para alcanzar este objetivo. Lo hacemos de manera automática. Lo mismo ocurre cuando tenemos que subirnos a un automóvil, cuando tenemos que lustrar nuestros zapatos, cuando nos calzamos, cuando nos vestimos, cuando tenemos que cambiar desafortunadamente la llanta de un automóvil o, simplemente cuando queremos tomar un vaso con agua.
Veamos un ejemplo de algoritmo que es muy conocido para todos nosotros y recibe el nombre de receta de cocina.Pechuga de pollo en salsa de elote y chile poblano.
Ingredientes (para seis personas)
3 pechugas deshuesadas, sin piel y partidas a la mitad.
1 diente de ajo.
4 gramos de pimienta negra.
Sal.
6 cucharadas de aceite.
5 chiles poblanos asados y limpios.
½ tasa de leche.
¼ tasa de crema de elote.Algoritmo (Preparación).
• Muela el ajo, la pimienta y un poco de sal y únteselo a las pechugas.
• Caliente el aceite y dore las pechugas.
• Licue los chiles con la leche y la crema, y mézclelos con la crema de elote.
• En una fuente coloque las pechugas y báñelas con la mezcla anterior.
• Cubra el platón con papel aluminio y hornee a 2000 C, durante 15 minutosEn resumen, todo algoritmo debe ser:
• Preciso. Indicando el orden de realización de cada uno de los pasos.
• Definido. Si se sigue el algoritmo varias veces proporcionándole los mismos datos, se deben obtener los mismos resultados.
• Finito. Al seguir el algoritmo, éste debe terminar en algún momento, es decir, tener un número finito de pasos.
1.2.2. Planteamiento de alternativas de solución.Para diseñar un algoritmo se debe comenzar por identificar las tareas más importantes para resolver el problema y disponerlas en el orden en que han de ser ejecutadas. Los pasos en esta primera descripción de actividades deberán ser definidos, añadiendo más detalles a los mismos e incluso, algunos de ellos, pueden requerir un refinamiento adicional antes de que podamos obtener un algoritmo claro, preciso y completo. En un algoritmo se deben de considerar tres partes:
• Entrada. Información dada al algoritmo.
• Proceso. Operaciones o cálculos necesarios para encontrar la solución del problema.
• Salida. Respuestas dadas por el algoritmo o resultados finales de los cálculos.Análisis del problema.
Datos de Salida: Platos limpios.
Datos de Entrada: Platos sucios.
Proceso: Prepara lo necesario para el lavado de platos, lavar platos mientras queda alguno sucio y luego secarlos.Algoritmo
Inicio
Abrir el grifo o llave del agua
Tomar el estropajo
Echarle jabón
Mientras quedan platos
Lavar el plato
Enjuagarlo
Dejarlo en el escurridor
Mientras quedan platos en el escurridor.
Secar plato.
Fin.1.2.3. Elección de una alternativa.
1.2.4. Desarrollo de la solución.
Observemos las siguientes características del algoritmo.
• Principia con la palabra inicio.
• La palabra Mientras se usa para actividades que se van a segur realizando “mientras se cumpla la condición establecida: queden platos.
• Para distinguir las actividades incluidas en el mi9entras se amplia su margen.
• Termina con la palabra Fin.Veamos un ejemplo con un algoritmo un poco más grande. Algoritmo para ir al cine.
Análisis del problema
Datos de Salida: Ver la película.
Datos de entrada: Nombre de la película, dirección de la sala, hora de proyección.
Proceso: Seleccionar una película de la cartelera del periódico, ir a la sala y comprar la entrada la entrada para, finalmente, poder ver la película.Algoritmo
Inicio
//seleccionar la película –comentario para identificar el proceso
tomar el periódico
mientras no lleguemos a la cartelera
pasar la hoja
mientras no se acabe la cartelera
leer la película
si nos gusta, recordar el título
elegir una de las películas entre las que nos gustaron
leer la dirección de la sala y la hora de proyección.//comprar la entrada –otro comentario
trasladarse a la sala
si no hay entradas, ir al fin
si hay fila de espera
ponerse al final de la fila
mientras no lleguemos a la taquilla
avanzar
si hay entradas, comprar la entrada
si no ir al fin
//ver la película –comentario
buscar asiento
sentarse
ver la película
fin.1.2.5. Evaluación de la solución.
Observamos nuevas características en este algoritmo.
• Se usan dobles diagonales (//) para separar las instrucciones en bloque. Son comentarios que nos permiten entender más fácilmente cuáles son las tareas más importantes que conforman el algoritmo. Estos se pueden usar luego para dividir el programa en módulos.
• Se usa la palabra si para decidir entre realizar una acción o no dependiendo de la condición establecida: ¿Hay fila de espera? Entonces nos ponemos al final de la misma.
• En ocasiones “si” va acompañada de “sino” que a diferencia de la anterior permite elegir entre dos acciones.
• Los “si” pueden contener dentro de sí a los “mientras” y a la inversa.
• Los márgenes nos permiten distinguir cuáles instrucciones pertenecen solamente al “si” y también al “mientras” dentro del “si”.
1.2.6. ACTIVIDADES DE REFORZAMIENTO
1.3.1. Diagramas de entrada-proceso-salida.
ENTRADA-PROCESO- SALIDA
En esta sección, se darán a conocer algunos los mecanismos básicos para interactuar con un sistema. Como ejemplo de una aplicación visual, los procesadores de texto presentan al usuario una hoja en blanco, los sistemas de hojas de cálculo interactúan mediante libros, hojas y celdas. Así mismo dichas aplicaciones cuentan con formas para que el usuario modifique tipos de fuente, cambie configuraciones, guarde, asigne nombres a archivos, etc. Toda la información que el usuario necesite ingresar al sistema, lo hará a través de botones, cajas donde ingresará texto, cuadros combinados para seleccionar opciones, botones radio o cajas de selección. A su vez, el sistema proporciona mensajes y emite resultados ya sea en ventanas de mensajes hechas ex profeso, en etiquetas, en cuadros de impresión, en las etiquetas de los botones, etc. Las posibilidades de ingreso y emisión de resultados son variadas.
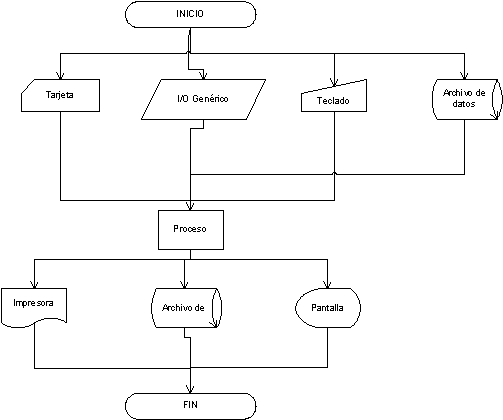
El problema básicamente se puede resumir de manera simplista en hacer que la aplicación tome información del usuario, haga un procesamiento de la misma e imprima de manera visible algún resultado. A los datos que el usuario proporcione, se le llamarán datos de entrada y a la acción que el programa ejecute para mostrar sus resultados se le dará el nombre de datos de salida. Tradicionalmente a esto en computación se le conoce como proceso de entrada/salida (I/O, input/output). El siguiente diagrama de flujo muestra de manera esquemática cómo se representan diferentes técnicas de entrada y salida:
Fig. 1 .- Diagrama de entrada-proceso-salida
Se tiene que tomar con cautela lo que se representa en un diagrama de flujo con respecto a la entrada y salida de información, sobre todo para aplicaciones visuales. En la figura se muestra que la entrada de datos puede ser a través de tarjetas perforadas, teclado o archivo en disco, sin embargo esto es un esquema muy simplificado, ambiguo y no se debe tomar de manera literal. Para ilustrar lo anterior tómense los siguientes ejemplos:
• En la actualidad, ya no existen entradas de tipo tarjeta perforadas, sin embargo el código de barras se podría considerar como el sucesor de dicho sistema. Mas bien, el símbolo correspondiente se ha utilizado por tradición para representar entrada del usuario.
• El acceso por teclado puede estar dirigido a una caja de texto, un cuadro combinado, un botón de radio, etc.
• La entrada de datos por archivo puede referirse a archivo de texto ASCII sencillo, ANSI, con un tipo propio, una celda en una hoja de cálculo, una tabla en una base de datos, etc.
• Para la salida en pantalla, no se especifica en cuál formulario, caja de texto, etiqueta, campo de impresión, etc., se realizará dicha salida.
• Como en el caso de la entrada vía archivo, la salida a archivo que se muestra en la figura tampoco especifica el tipo del referido archivo.
• Aunque se puede enviar directamente a una impresora, por tradición la salida impresa se podría utiliza para representar la salida del sistema a pantalla a algún objeto en particular.
Los diagramas de flujo representan la forma más tradicional para especificar los detalles algorítmicos de un proceso. Se utilizan principalmente en programación, economía y procesos industriales; estos diagramas utilizan una serie de símbolos con significados especiales. Son la representación gráfica de los pasos de un proceso, que se realiza para entender mejor al mismo. Son Modelos tecnológicos utilizados para comprender los rudimentos de la programación lineal
Otra definición del diagrama de flujo es la siguiente:
"Es un esquema para representar gráficamente un algoritmo. Se basan en la utilización de diversos símbolos para representar operaciones específicas. Se les llama diagramas de flujo porque los símbolos utilizados se conectan por medio de flechas para indicar la secuencia de operación. Para hacer comprensibles los diagramas a todas las personas, los símbolos se someten a una normalización; es decir, se hicieron símbolos casi universales, ya que, en un principio cada usuario podría tener sus propios símbolos para representar sus procesos en forma de Diagrama de Flujo. Esto trajo como consecuencia que solo aquel que conocía sus símbolos, los podía interpretar. La simbología utilizada para la elaboración de diagramas de flujo es variable y debe ajustarse a un patrón definido previamente."
Diagrama de flujo en el cual se emplean los símbolos más comunes
Principales simbolos
No es indispensable usar un tipo especial de símbolos para crear un diagrama de flujo, pero existen algunos ampliamente utilizados por lo que es adecuado conocerlos y utilizarlos, ampliando así las posibilidades de crear un diagrama más claro y comprensible para crear un proceso lógico y con opciones múltiples adecuadas.
- Flecha . Indica el sentido y trayectoria del proceso de información o tarea.
- Rectángulo . Se usa para representar un evento o proceso determinado. Éste es controlado dentro del diagrama de flujo en que se encuentra. Es el símbolo más comúnmente utilizado.
- Rectángulo redondeado. Se usa para representar un evento que ocurre de forma automática y del cuál generalmente se sigue una secuencia determinada.
- Rombo . Se utiliza para representar una condición. Normalmente el flujo de información entra por arriba y sale por un lado si la condición se cumple o sale por el lado opuesto si la condición no se cumple. Lo anterior hace que a partir de éste el proceso tenga dos caminos posibles.
- Círculo . Representa un punto de conexión entre procesos, se utiliza cuando es necesario dividir un diagrama de flujo en varias partes, por ejemplo por razones de espacio o simplicidad. Una referencia debe de darse dentro para distinguirlo de otros. La mayoría de las veces se utizan números en los mismos.
Existen además una variedad de formas especiales para denotar las entradas, las salidas, los almacenamientos, etcétera.
Reglas
De acuerdo al estándar ISO los símbolos e incluso las flechas deben de tener ciertas características para estar dentro del estándar. En el caso se los círculos de conexión se debe usar sólo cuando se conecta con un proceso contenido dentro de la misma hoja.
Aunque también existen conectores de página los cuales son como una casita y se utilizan para unir actividades que se encuentran en otra hoja.
- Existe siempre un camino que permite arribar a una solución
- Existe un único inicio del proceso
- Existe un único punto de fin para el proceso
- De cada símbolo solo puede salir una flecha de flujo, salvo del rombo que indica una comparación con dos caminos posibles
1.3.3. Ejemplos de usos y aplicación.
EJEMPLOS.
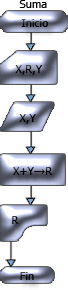
SUMA DE DOS NUMEROS
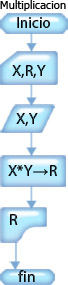
MULTIPLICACIÓN DE DOS NUMEROS
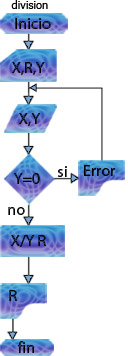
DIVISION DE DOS NUMEROS
1.3.4. ACTIVIDADES DE REFORZAMIENTOJoyanes, Luis. Fundamentos de programación, algoritmos y estructura de datos. México. Mc. Graw Hill, 2000.
Pérez, M.J. Informática II para Bachillerato. México. Alfaomega Grupo Editor, 2004.
Vasconcelos, Jorge. Introducción a la computación. México. Publicaciones Cultural, 2002.
www.es.wikimedia.org
www.mis-algoritmos.com
www.uady.mx